PDF] New parametrization of $A^2+B^2+C^2=3D^2$ and Lagrange's four-square theorem
Por um escritor misterioso
Last updated 26 dezembro 2024
![PDF] New parametrization of $A^2+B^2+C^2=3D^2$ and Lagrange's four-square theorem](https://d3i71xaburhd42.cloudfront.net/40890436b6511a579be57c676d175ebbd8293125/1-Table1-1.png)
In this paper we provide a new parametrization for the diophantine equation $A^2+B^2+C^2=3D^2$ and give a series of corollaries. We discuss some connections with Lagrange's four-square theorem. As applications, we find new parameterizations of equilateral triangles and regular tetrahedrons having integer coordinates in three dimensions.
![PDF] New parametrization of $A^2+B^2+C^2=3D^2$ and Lagrange's four-square theorem](https://pubs.acs.org/cms/10.1021/acs.jctc.1c00953/asset/images/acs.jctc.1c00953.social.jpeg_v03)
Analyzing the Behavior of Spin Phases in External Magnetic Fields
![PDF] New parametrization of $A^2+B^2+C^2=3D^2$ and Lagrange's four-square theorem](https://upload.wikimedia.org/wikipedia/commons/thumb/8/8a/Quintic_polynomial.svg/1200px-Quintic_polynomial.svg.png)
Quintic function - Wikipedia
![PDF] New parametrization of $A^2+B^2+C^2=3D^2$ and Lagrange's four-square theorem](https://media.springernature.com/full/springer-static/image/art%3A10.1038%2Fs41467-023-41214-9/MediaObjects/41467_2023_41214_Fig1_HTML.png)
Efficient optimization with higher-order ising machines
![PDF] New parametrization of $A^2+B^2+C^2=3D^2$ and Lagrange's four-square theorem](https://geelaw.blog/entries/lagrange-4sq-thm/assets/hero.png)
Chit-chat on Lagrange's four-square theorem
![PDF] New parametrization of $A^2+B^2+C^2=3D^2$ and Lagrange's four-square theorem](https://pubs.acs.org/cms/10.1021/acs.jpcb.2c04649/asset/images/acs.jpcb.2c04649.social.jpeg_v03)
Computational Modeling of RNA Aptamers: Structure Prediction of
![PDF] New parametrization of $A^2+B^2+C^2=3D^2$ and Lagrange's four-square theorem](https://www.mdpi.com/files/uploaded/covers/mathematics/big_cover-mathematics-v10-i24.png)
Mathematics December-2 2022 - Browse Articles
![PDF] New parametrization of $A^2+B^2+C^2=3D^2$ and Lagrange's four-square theorem](https://i1.rgstatic.net/publication/2521952_Using_Quaternions_for_Parametrizing_3-D_Rotations_in_Unconstrained_Nonlinear_Optimization/links/635624f26e0d367d91be8d2e/largepreview.png)
PDF) Using Quaternions for Parametrizing 3-D Rotations in
![PDF] New parametrization of $A^2+B^2+C^2=3D^2$ and Lagrange's four-square theorem](https://d3i71xaburhd42.cloudfront.net/40890436b6511a579be57c676d175ebbd8293125/1-Table1-1.png)
PDF] New parametrization of $A^2+B^2+C^2=3D^2$ and Lagrange's four
![PDF] New parametrization of $A^2+B^2+C^2=3D^2$ and Lagrange's four-square theorem](https://pubs.acs.org/cms/10.1021/acs.jctc.2c00460/asset/images/medium/ct2c00460_0012.gif)
When Gold Is Not Enough: Platinum Standard of Quantum Chemistry
![PDF] New parametrization of $A^2+B^2+C^2=3D^2$ and Lagrange's four-square theorem](https://www.mdpi.com/mathematics/mathematics-10-04395/article_deploy/html/images/mathematics-10-04395-g001.png)
Mathematics, Free Full-Text
![PDF] New parametrization of $A^2+B^2+C^2=3D^2$ and Lagrange's four-square theorem](https://img.yumpu.com/12104273/1/500x640/multivariable-calculus-reed-college.jpg)
Multivariable Calculus - Reed College
![PDF] New parametrization of $A^2+B^2+C^2=3D^2$ and Lagrange's four-square theorem](https://media.springernature.com/m685/springer-static/image/art%3A10.1007%2Fs10208-022-09553-z/MediaObjects/10208_2022_9553_Fig5_HTML.png)
Construction of $$C^2$$ Cubic Splines on Arbitrary Triangulations
Recomendado para você
-
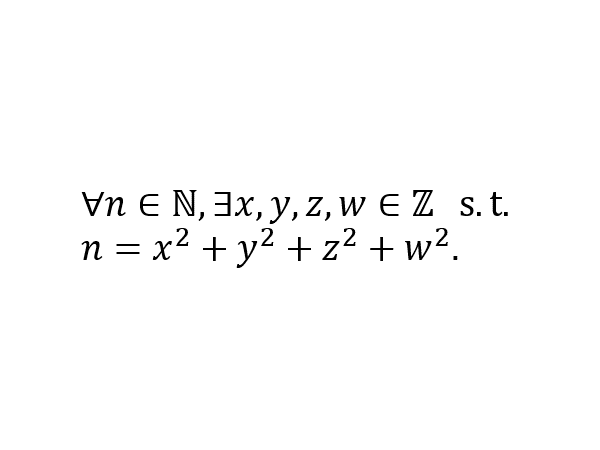 Chit-chat on Lagrange's four-square theorem26 dezembro 2024
Chit-chat on Lagrange's four-square theorem26 dezembro 2024 -
 Sums of four squares — AnhThu Nguyen26 dezembro 2024
Sums of four squares — AnhThu Nguyen26 dezembro 2024 -
Jacobi's four-square theorem - Wikipedia26 dezembro 2024
-
 m 8.35 (Lagrange's Four-Square Theorem) If n is a26 dezembro 2024
m 8.35 (Lagrange's Four-Square Theorem) If n is a26 dezembro 2024 -
 What's so interesting about squared numbers? Lagrange's Four Square Theorem26 dezembro 2024
What's so interesting about squared numbers? Lagrange's Four Square Theorem26 dezembro 2024 -
 Lagrange's four-square theorem26 dezembro 2024
Lagrange's four-square theorem26 dezembro 2024 -
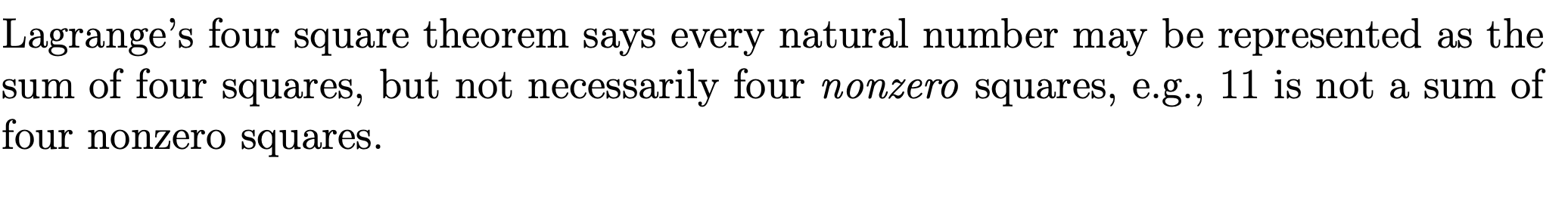 Solved Lagrange's four square theorem says every natural26 dezembro 2024
Solved Lagrange's four square theorem says every natural26 dezembro 2024 -
CodeChef - Lagrange's four-square theorem, also known as Bachet's conjecture, states that every natural number can be represented as the sum of four integer squares. This theorem was proven by Joseph Louis26 dezembro 2024
-
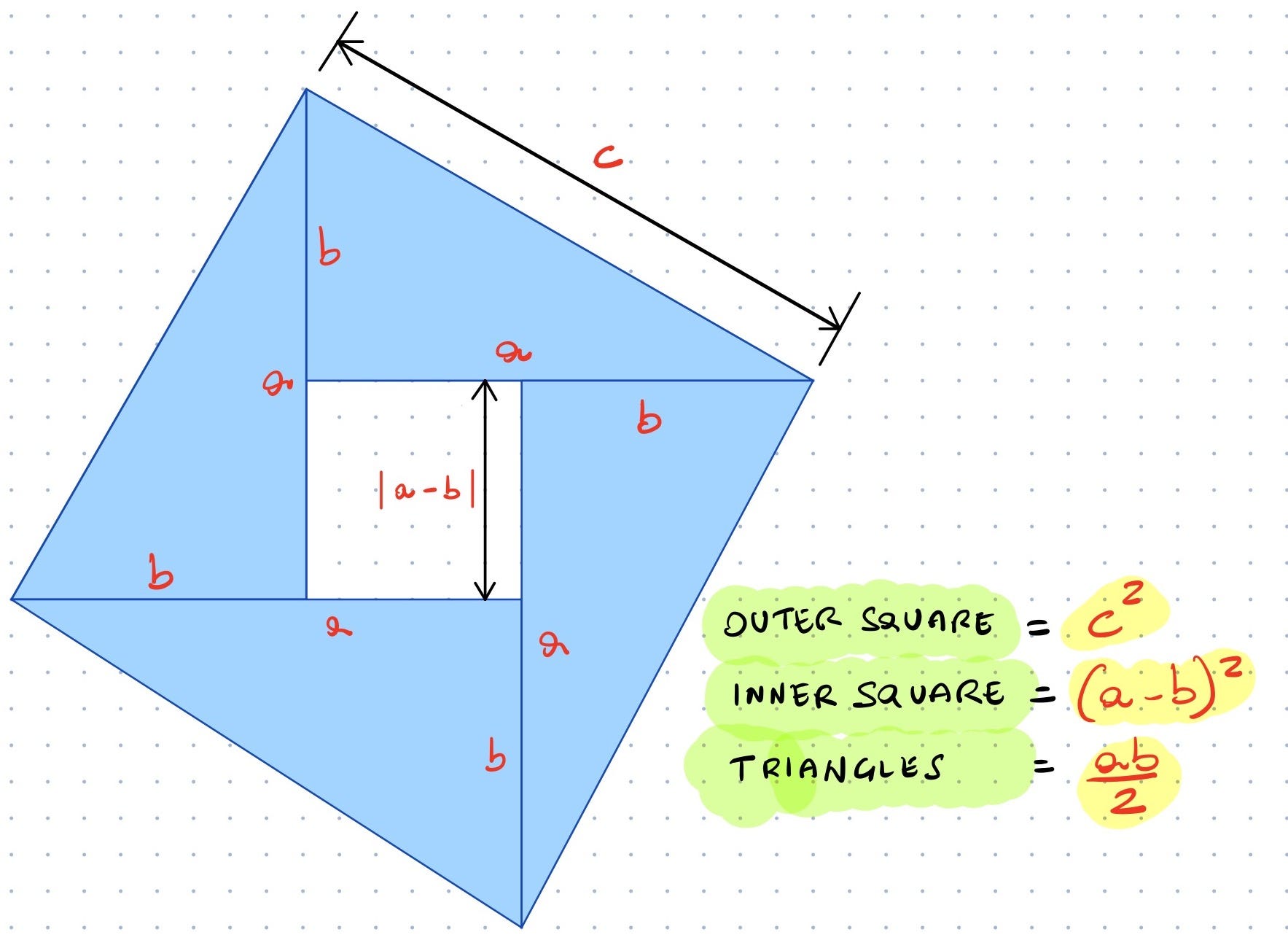 Proving the Pythagorean Theorem. Some algebraic and geometric proofs of…, by Michele Diodati, Not Zero26 dezembro 2024
Proving the Pythagorean Theorem. Some algebraic and geometric proofs of…, by Michele Diodati, Not Zero26 dezembro 2024 -
Waring's Problem -- from Wolfram MathWorld26 dezembro 2024
você pode gostar
-
 Hide and Seek (2005) - IMDb26 dezembro 2024
Hide and Seek (2005) - IMDb26 dezembro 2024 -
 Need for Speed: Rivals (preowned) - Xbox One - EB Games Australia26 dezembro 2024
Need for Speed: Rivals (preowned) - Xbox One - EB Games Australia26 dezembro 2024 -
 Pokemon Emerald Cheats: Power up Your Gameplay!26 dezembro 2024
Pokemon Emerald Cheats: Power up Your Gameplay!26 dezembro 2024 -
 Craig David - Friday Night (Official Audio)26 dezembro 2024
Craig David - Friday Night (Official Audio)26 dezembro 2024 -
 Hudson reporting for duty: The tough-as-nails CIA legend hits the field in Season Five Reloaded — news.community.zeus — Blizzard News26 dezembro 2024
Hudson reporting for duty: The tough-as-nails CIA legend hits the field in Season Five Reloaded — news.community.zeus — Blizzard News26 dezembro 2024 -
 Racismo e o Dia Internacional da Mulher Negra Latino-Americana e Caribenha - O Mundo Autista26 dezembro 2024
Racismo e o Dia Internacional da Mulher Negra Latino-Americana e Caribenha - O Mundo Autista26 dezembro 2024 -
 ShapeDiver - squid text lines are missing and image can not be26 dezembro 2024
ShapeDiver - squid text lines are missing and image can not be26 dezembro 2024 -
 9+ Antonyms of Wild with Meaning and Examples26 dezembro 2024
9+ Antonyms of Wild with Meaning and Examples26 dezembro 2024 -
![How To Pixel Art Tutorials [13] - Draw 32x32 Character (Part 1](https://i.ytimg.com/vi/ExRm4HvRIHA/sddefault.jpg) How To Pixel Art Tutorials [13] - Draw 32x32 Character (Part 126 dezembro 2024
How To Pixel Art Tutorials [13] - Draw 32x32 Character (Part 126 dezembro 2024 -
Persona 5 Royal is landing on Game Pass for PC day one26 dezembro 2024



